Brent Ozar recently ran a salary survey for people working with databases, and posted an article: Female DBAs Make Less Money. Why?
Many of the responses were along the lines of “Well, duh.” I, personally, felt much of the same thing.
But, I think with something like this, there is a risk for confirmation bias. If you already believed that women were underpaid, there is a chance that you’ll see this as more proof and move on, without ever questioning the quality of the data.
What I want to do is try to take a shot at answering the question: How strong is this evidence? Does this move the conversation forward, or is it junk data?
Consider this blog post an introduction into some statistics and working with data in general. I want to walk you through some of the analysis you can do once you start learning a little bit of statistics. This post is going to talk a lot more about how we get to an answer instead of what the answer is.
Data Integrity
So, first we want to ask: Is the data any good? Does it fit the model we would expect? Barring any other information I would expect it to look similar to a normal distribution. A lot of people around the center, with roughly even tails on either side, clustered reasonably closely.
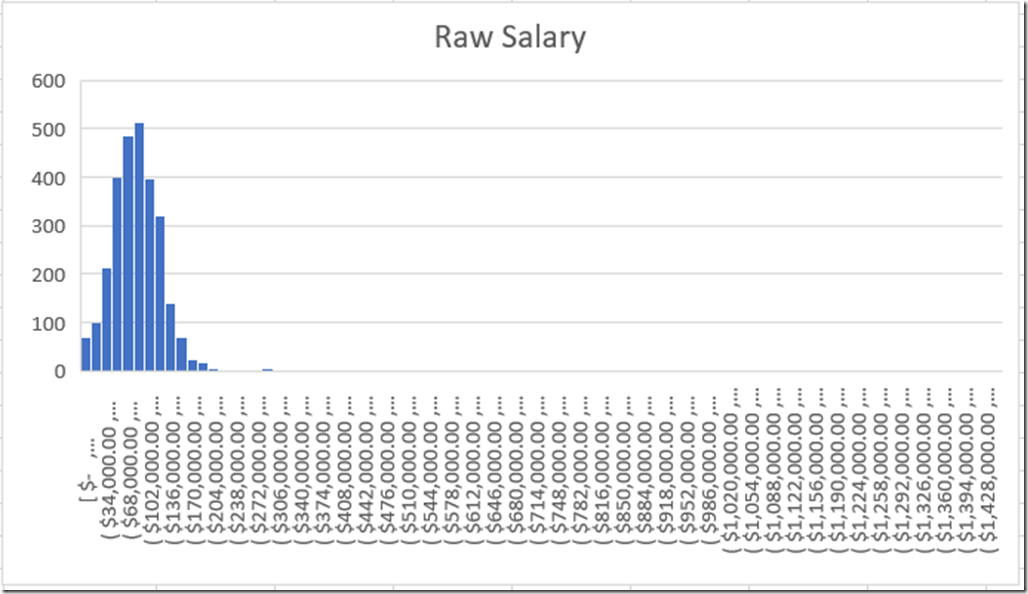
So if we just take a histogram of the raw data, what do we get?
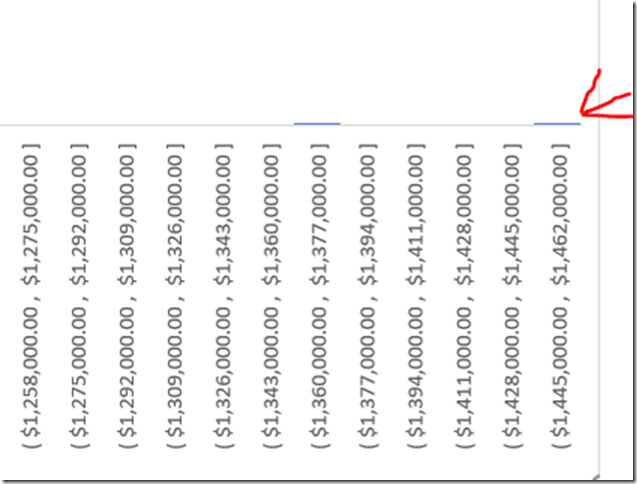
So, we’ve got a bit of a problem here. The bulk of the data does look like a normal distribution, or something close to it. But we’ve got some suspicious outliers. First we have some people allegedly making over a million dollars in salary. That’s why the histogram is so wide. Hold on, let me zoom in.
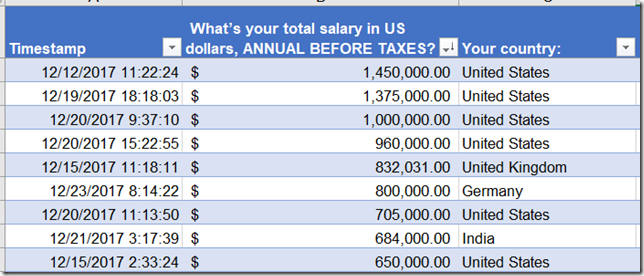
Even ignoring the millionaires, we have a number of people reporting over half a million dollars per year in salary.
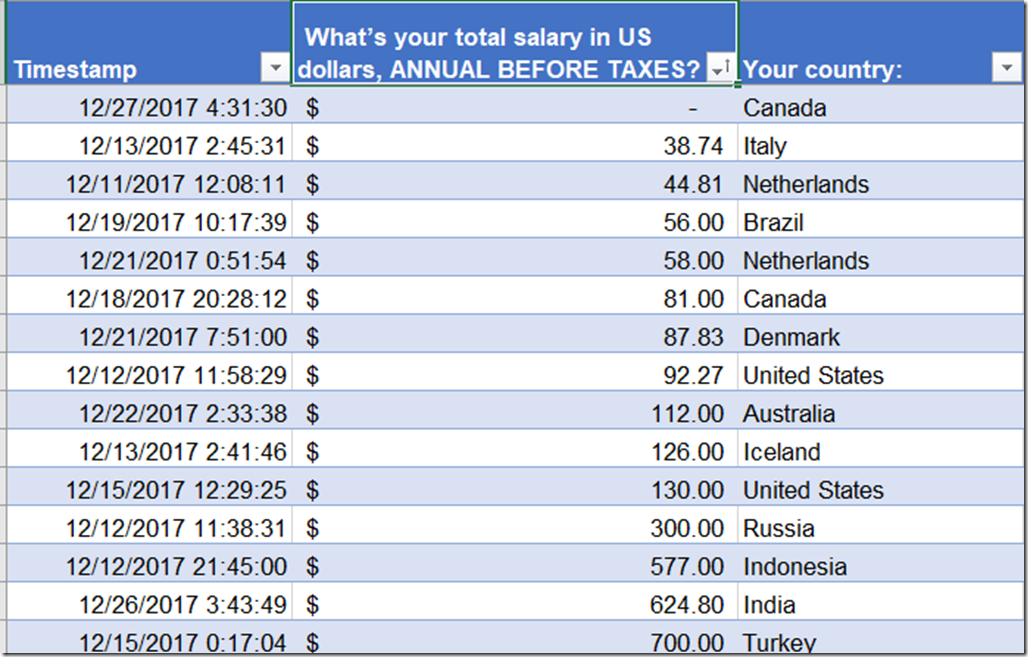
We’ve also got issues on the other end of the spectrum. Apparently there is someone in Canada who is working as an unpaid intern:
Is this really an issue?
Goofy outliers are an issue, but the larger the dataset the smaller the issue. If Bill Gates walks into a bar, the average wealth in the bar goes up by a billion. If he walks into a football stadium, everyone gets a million dollar raise.
One way of looking at the issue is to compare the median to the mean. The median is the salary smack dab in the middle, whereas mean is what we normally think of when we think of average.
The median doesn’t care where Bill Gates is, but the mean is sensitive to outliers. If we compare the two, that should give us an idea if we have too much skew in either direction.
So, if we take all of the raw data we get a $4,000 difference. That feels significant, but could just be the way is naturally skewed. Maybe all the entry level jobs are around the same, but the size of pay raises get bigger and bigger at the top end.
Averages after removing outliers
Okay, well lets take those outliers out. We are going to use $15,000-$165,000 as a valid range for salaries. Later on I’ll explain where I got that range.
There are 143 entries outside of that range, or about 5% of the total entries. I feel comfortable excluding that amount. So what’s the difference now?
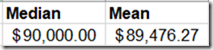
So the middle hasn’t moved, but the mean is about the same now. So this tells me that salaries are evenly distributed for the most part, with some really big entries towards the high end. Still, the $4,000 shift isn’t too big, right?
Wait, this actually is an issue…
Remember when I said 2 seconds ago that $4,000 was a significant but not crazy large? Well, unfortunately the skew in the data set really screws up some analysis we want to do. Specifically, our friend Standard Deviation. We need a reasonable standard deviation to do a standard error analysis, which we cover later.
Standard Deviation is a measure of the spread of a distribution. Are the numbers clumped near the mean, or are they spread far out? The larger the standard deviation, the more variation of entries.
If a distribution is a roughly normal distribution, we can predict how many results will fall within a certain range: 68% within +/- 1 standard deviation, 95% within +/- 2 deviations, 99.7% within 3 deviations.
Well, because of the way standard deviation is calculated, it is especially sensitive to outliers. In this case, it’s extremely sensitive. The standard deviation of all the raw data is $66,500 . When I remove results outside of $15-$165K, the standard deviation plummets to $32,000. This suggests that there is a lot of variability in the data being caused by 5% of the entries.
So let’s talk about how to remove outliers.
Removing Outliers
Identifying the IQR
Remember when I got that $15,000-$165000 range? That’s by using a tool called InterQuartile Range or IQR.
It sounds fancy, but it is incredibly simple. Interquartile range is basically the distance between the middle of the bottom half and the middle of the top half.
So in our case, if we take the bottom half of the data, the median salary is $65,000. If we take the top half of the data, the median salary is $115,000. The IQR is the difference between the two numbers, which is $50,000.
Using IQR to filter out outliers
Okay, so we have a spread $50,000 between the first and third quartiles. How do we use that information? Well there is a common rule of thumb that anything outside +/- 1.5 IQR is an outlier. In fact, when you see a boxplot, that is what is going on when you see those dots.
So, $50,000 *1.5 is $75,000. If we take the median ($90,000) and add/subtract 75,000 we get our earlier range of $15,000-$165,000
Standard Error Analysis
Okay, so why did we go through all that work to get the standard deviation to be a little more reasonable? Well, I want to do something called a Standard Error Analysis to answer the following question:
What if our sample is a poor sample?
What is our average female salary is lower because of a sampling error? Specifically, what are the odds that we samples a lower average salary by pure chance? “Poppycock!”, you might say. Well, standard error gives us an idea of how unlikely that is.
Importance of sample size
Let’s say there are only 1,000 female DBAs in the whole world, and we select 10 of them. What are the chances that the average salary of those 10 is representative of the original 1,000? It’s not great. We could easily pick 10 individuals from the bottom quartile, for example.
What if we sampled 100 instead of 1000? The chances get a lot better. We are far more likely to include individuals that are above average for the population as a whole. The larger the sample, the closer the sample mean will match the mean of the original population.
The larger the sample size, the smaller the standard error.
Importance of spread
Remember before we said that a reasonable standard deviation is important? Let’s talk about why. Let’s say there are 10 people in that bar, and that the spread of salaries is small. Everyone there make roughly the same amount. As a result the standard deviation, a measure of spread, is going to be quite small.
So, let’s say you take three people at random out of that bar, bribe them with a free drink, and take the average of their salaries. If you do that multiple times, in general that number is going to be close to the true average of the whole population (the bar).
Now, Bill Gates walks in again and we repeat the exercise three times. Because he is such an outlier, the standard deviation is much larger. This throws everything out of whack. We get three samples: $50,000, $60,000, and $30,000,000,000. Whoops.
The smaller the standard deviation of a population, the smaller the standard error.
Calculating Standard Error
Getting the prerequisites
To calculate the standard error, we need mean, standard deviation and sample size. Before we calculate those numbers, I want to narrow the focus a bit.
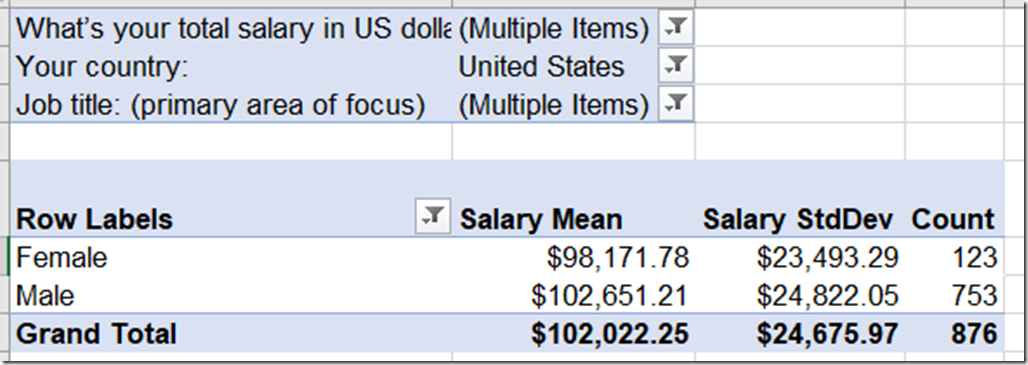
I’ve taken the source data, and narrowed it down to US, DBA and within $15,000-$16,5000. This should give us more of an apples to apples comparison. So what do we get?
We’ve got a gap in average salary of about $4,500. This seems quite significant, but soon we’ll prove how significant.
We’ve also a standard deviation of around $24,500. If salaries full under a normal distribution, this means that 95% of DBA salaries in the US should be within $52,500-$151,000. That sounds about right to me.
Calculating individual standard error
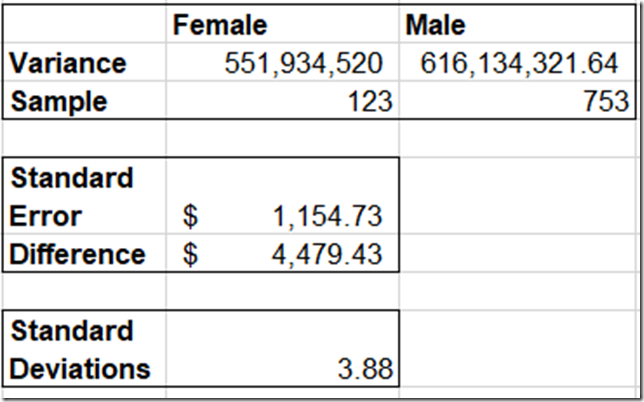
So now we have everything we need to calculate standard error for the female and male samples individually. The formula for standard error is standard deviation divided by the square root of the count.
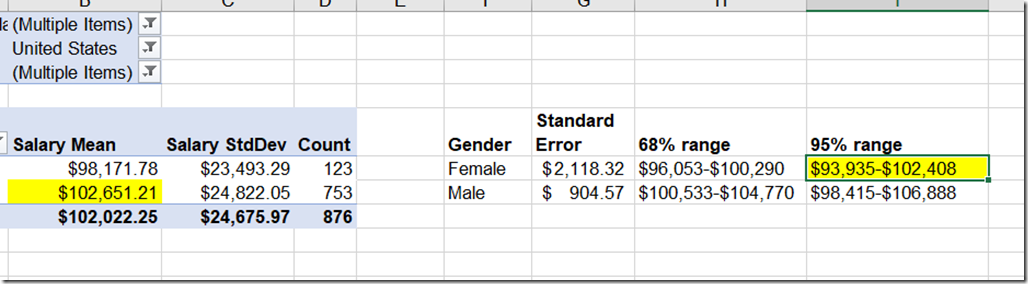
So for females, it’s 23,493 / sqrt(123) = 2118. This means that if we were only sampling female DBAs, we would expect the average salary to be within +/- $2,118 about two thirds of the time.
So, if we were to randomly sample female DBA’s, then 95% of the time, that sample’s average would be less than the male average from before.
That seems like a strong indicator that the lower average salary for females isn’t just chance. But we actually have a stronger way to do this comparison.
Standard error of sample means
Whenever you want to compare the means from two different samples, you use a slightly different formula which combines everything together.
The formula is SQRT( (Sa^2 + Sb^2) / (na +nb)) . S is the standard deviation for samples a and b. Standard deviation squared is also known as the variance. N is the count for samples a and b.
If we combine it all together we get this:
The standard error when we combine samples is $1,154. This indicates that if there was no difference between the distribution in female and male salaries, then 68% of the time they would be within $1,154.
Well in this case, the difference in means is almost 4 times that. So if the difference in means is 3.88 standard deviations apart, how often would that happen by pure chance? Well, we would see this level of separation 0.01% of the time, or about 1 in 10,000.
Conclusion
I take this as strong evidence that there is a real wage gap between female and male DBAs in the USA.
What this does not tells us is why. There are a number of reasons that people speculate as to the cause of this gap, many in Brent’s original blog post and the comments below it. I’ll leave that to them to speculate what the cause is.
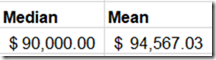

WOW! That’s a lot of numbers in that there post. 😀
It sounds smart to me – one tweak though. I do know DBAs making over $165k, although the catch is that they’re usually in very high-pressure environments (freelance DBA consultants, DBAs at hedge funds, etc.) There’s not a lot, but it’s enough that it didn’t raise my eyebrows too far.
Yeah, that’s a very good point. >165K was about 3% of the responses. Large enough to be real, but likely outside the norm for most DBAs.
That being said DBA work definitely seems to skew towards the high end. If you are at the top of your field, you can make a LOT of money.
Given the fact that the range of both men and women overlap: we cannot say that their means are not the same. I think that a two means t-test would have been more appropriate in this case.
An interesting metric would have been to know how much men and women hourly rate differs.
To have such a negligible difference is quite interesting given the fact that women DBA take more time off or are more likely to take part-time position in order to cater for their family needs.
Hi Cyrille, thanks for the feedback, I really appreciate it.
Could you clarify what you mean when you say “Given the fact that the range of both men and women overlap: we cannot say that their means are not the same.”? I’m not sure if I completely understand where you are coming from; I think I’m missing something.
If you are saying that it’s always possible for the means to be the same, then I definitely agree with you. But I believe we can determine that possibility to be exceedingly small if we have a large enough sample size. In this case, I’m calculating the chances of them being the same is 1 in 1000. I’m having trouble understanding how an overlap in range would prevent that sort of statement from being valid.
Regarding the two means t-test, it looks like it uses the same exact formula for the test statistic, but uses a t-distribution for the critical value instead of a normal distribution. So the question is: do you feel a t-distribution makes more sense in this case? I’d be curious to know, since I’m still learning about t-distributions.
What is also not considered is the age of the participants. Maybe the bulk of the women’s age are lower than the bulk of the men, which easily can explain the difference in salary.
Hi Albertus, there are definitely a large number of possible causes for the discrepancy. One of the nice things is the raw data is freely available, so you take a look for yourself. While age isn’t part of the data set, number of years working with databases is available and is a decent proxy.
It’s worth repeating that this analysis only shows that the discrepancy is not purely caused by sampling error. It doesn’t give any indication to the actual cause.
The means test using a t-distribution is a valid approach. The t-distribution progressively approaches a normal distribution as the degrees of freedom increase.
Thanks for the feedback! So, if I’m understanding correctly, when your sample size is sufficiently large a t-distribution is roughly the same as a normal distribution. When you have a smaller sample size, the t-distribution takes that into account better. I’ll definitely run the numbers again using a two means t-test and see what the difference is.
Is it a true Normal Distribution, or is it a Log-Normal Distribution, owing to the fact that you can’t have negative salaries, while positive salaries are unbounded? Would it significantly change things?
Hi Zac, I suspect you are right that it’s not a true Normal Distribution. In this case I was eyeballing that it looks *close* to a normal distribution, but it almost certainly fits something slightly different. That’s going to have some sort of impact, but I’m hoping by removing the outliers, we help address that.
That being said, that shouldn’t matter too much for the analysis here. With standard error, you don’t need a normal distribution for it to work. Whatever distribution of the population, the *sampling* distribution will approach a normal one as your average sample size increases.
So as far as I’m aware, we can still say that it’s unlikely that the discrepancy is caused purely by sampling error.
Interesting read and well written! Thnx!
Hi Eugene, the way I would personally compare two sample means, is by hypothesis testing. I would start by setting my first hypothesis as stating that both means of men and women are equal. The opposite hypothesis is that both means are not equal. I then run a 2 sample t-test to check which hypothesis is valid.
Using Python and doing similar data cleaning as you did (keep the salaries within the range of 15,000-165,000, Country = USA, JobType=DBAs) I got slightly different means (male= 102,933, female=98,252) for 139 data points for females and 820 data points for males.
The t-test give me a p value of 0.069 which is greater than 95%. Therefore we cannot affirm that men and women don’t have an equal mean salary (there is 7% that they have the same mean). If we keep the outliers we can however says that men and women are not paid the same (p=0.02).
From the data, it seems that men and women are paid equally in normal employment. But a small amount of men having accepted more responsibilities (they have their own company) or more stressful jobs are much better paid than the rest. They are the outliers.
Hi Eugene, that’s a great post.
Thanks for running the numbers.
I’d be interested in seeing if there’s anyway of accounting for parenthood in future versions of this. My hypothesis being that parenthood has a greater effect on women’s careers than men’s.
There was an article about the New York times that talks a little bit about the impact:
https://www.nytimes.com/2014/09/07/upshot/a-child-helps-your-career-if-youre-a-man.html
I think one of the challenges is teasing out how much is outright discrimination and assumptions about mothers; versus secondary impacts of being a parent (less capacity for overtime, etc).
When interpreting this data, one needs to remember that this is a self-selected sample population, which comes with inherent statistical errors.
Statistics students are warned of the dangers of inference from such populations, because the sampled population is less likely to represent the total population for which we are trying to make a statistical determination.
Randomized selection of a population sample is a crucial part of conducting experimental design in statistics, see
https://introductorystats.wordpress.com/2011/03/09/design-of-experiments/
Also from Wikipedia: (https://en.wikipedia.org/wiki/Self-selection_bias)
“Self-selection makes determination of causation more difficult. For example, when attempting to assess the effect of a test preparation course in increasing participant’s test scores, significantly higher test scores might be observed among students who choose to participate in the preparation course itself. Due to self-selection, there may be a number of differences between the people who choose to take the course and those who choose not to, such as motivation, socioeconomic status, or prior test-taking experience. Due to self-selection according to such factors, a significant difference in mean test scores could be observed between the two populations independent of any ability of the course to effect higher test scores. An outcome might be that those who elect to do the preparation course would have achieved higher scores in the actual test anyway. If the study measures an improvement in absolute test scores due to participation in the preparation course, they may be skewed to show a higher effect. A relative measure of ‘improvement’ might improve the reliability of the study somewhat, but only partially.
Self-selection bias causes problems for research about programs or products. In particular, self-selection affects evaluation of whether or not a given program has some effect, and complicates interpretation of market research.”
That’s an important point and a good reminder. Thank you.
https://www.forbes.com/sites/karinagness/2016/06/30/new-report-men-work-longer-hours-than-women/#6bde8ac918b4
*men worked 8.2 hours compared to women working 7.8 hours
In my European country this is even higher:
If you work less than 36 hours a week, but more than 12, then you are considered as working part time. A high proportion of women in the Netherlands, approximately 74 percent, work part time.
So I looked at the Excel and the average woman works 43.27 hours and the average man works 43 hours, so that isn’t it? But there are about 10 times as many male managers as female and maybe part time workers take care of their children instead of “taking work with them to home” and filling in surveys on blogs? Looks like women need to ask for a raise regardless.
Even if there were a difference in average hours worked by gender, if you have both hours and gender available in the data you can control for hours worked. In my blog post Building a DBA Salary Calculator, Part 0: Initial findings, I start to do some of that. Based on my initial look, it seems like the gap is still there even after you factor out hours worked.
You have a good point, that other people have made as well, that an internet survey in no way resembles a random study and is likely to have statistical errors.
Finally, saying that they need to ask for a raise has some challenges. There is an article talking about how women are likely to be punished for negotiating a higher salary. That seems to create a no-win situation for women.